Discussion Of The Vancura Factor
as applied to
Furnace
Regulation
A
Brief History Of Furnace Regulators:
Amps Mode: The amps-mode regulator was the first
regulator type to be developed. It was discovered, almost immediately that they
didn’t work very well. The
problems amps regulators exhibited were twofold. First, they did not start the
melting process smoothly and aggressively. When striking an arc on dry metal,
there exist only open circuits and short circuits. Before an arc is struck, the
electrodes move down to make contact with the steel. When the arc is struck all
of the electrodes move up to clear the short and the metal moves away by
melting. Neither condition is stable. This makes the bore-in process slow and timid. The second problem
occurred when the operator tried to run the furnace in single-phase mode (he’s
not supposed to do this but he does). The current through the two electrodes is
identical and one of the electrodes would dip into the bath undetected, and
cause a very unbalanced operating mode that wasted electricity, electrodes, and
sidewalls.
Difference Mode: Difference regulators were
introduced to fix the problems the amps regulator couldn’t handle. Initially,
it was determined that regulating to impedance would resolve the problems
plagued by the amps mode regulator, however, without modern electronics,
impedance was virtually impossible to implement. The difference regulator mimics
impedance regulation whenever the circuit is in balance, and is substantially
easier to build. The
difference regulator is sensitive to both voltage and current conditions and eliminates both
of the problems that the amps regulator exhibited. The voltage at the electrode
tip is a measure of the arc length, and holding the electrode voltage constant
assures that the electrodes are at a balanced distance from the bath. The
problem with the difference regulator is that it is sensitive to line voltage,
and the variation of line voltage affects the power input by the square of the
voltage change. As a result, some days the furnace runs too hot and other days
it runs too slow and eats up sidewall insulation. On the negative side, the
regulator wants to oscillate on a flat bath, which increases the electrode wear
and lowers the efficiency of power input. The difference regulator is very
difficult to tune and should be retuned as often as the line voltage changes.
The difference regulator becomes maintenance intensive. Difference
regulators are the most common type of regulator because they were easy to
design with crude electrical technology (relays and rheostats).
The difference regulator moves the electrodes down if the
voltage is too high and moves the electrodes up if the current is too high.
By scaling the voltage and current signals, one can effectively regulate to an
impedance set by the ratio of the voltage and current. The optimal operating impedance is
determined by the electrical characteristics of every element in the power grid powering the
system. This is no easy task and is often relegated to approximation.
Impedance Mode: The Impedance regulator became
available shortly after the computer revolution when Robicon® made the first
computerized regulator. The advantage of the impedance regulator over the
difference regulator is not well known because, over most of the operating
conditions, the operation is very similar. This regulator exhibits all of the
same characteristics as the difference regulator including the need for frequent
and difficult tuning. The Robicon regulator could be operated in either the impedance or
the difference mode. Most users used the difference mode because they trusted it
more.
Vancura Mode: Enter the Vancura regulator. The
Vancura regulator is designed to act as a difference or impedance regulator when
melting in on a fresh charge. This takes advantage of the aggressive melt in
characteristics of the difference regulator. It then gradually adjusts itself to
an amps regulator as the metal bath flattens out for optimal operation. The amps
regulator is more stable during a flat bath and that makes it possible to reduce
electrode wear and increase useful power input. Another advantage is that tuning
is simplified because only an amps setpoint is required at any point in the
operation. All of the other parameters except gain are normalized out of the
tuning process. The requirement of an extensive knowledge of the power grid
characteristics, electrical
relationships (volts, amps, and impedance), and other mathematical calculations are
eliminated. The amps mode also reduces the performance dependency on supply
voltage. Because the amps are generally held constant, any line voltage changes
affect the power input linearly rather than to the square of the line voltage change. This minimizes, if not eliminates, the need for
frequent maintenance
tuning.
In the regulator, the Vancura factor is manipulated by
taking advantage of a condition known as Standard Error. Standard Error is
equivalent to standard deviation except that the
deviation average is replaced by the amps setpoint value. This simplifies the
calculation process and offers a means to determine the state of the furnace
melt-in. Standard Error, for the Vancura factor, is calculated as the average
standard error for the three phases of current. The standard error value will
not generally exceed the setpoint amps and usually will not be lower than five
percent (5%) of the setpoint at flat bath (splashing metal in the arc plasma is the limiting
factor). The dubious practice of operating the furnace with one phase lifted
(single Phase) produces a standard error of at least 35%, which is sufficient to
maintain electrode balance.
Conclusion: By establishing a relationship between
standard error and the Vancura factor, the Vancura factor value will be
automatically varied over the course of the furnace operation from bore-down to
refining. This process optimizes regulation of the furnace to achieve lower
Kilowatt-Hours/Ton, shorter heat-to-heat time, and lower electrode wear. The
cost of electrodes, electricity, and time are the three most expensive costs in
the steel making process.
The
Math Behind The Vancura Factor:
Introduction: This document is meant to be a
discussion of how the Vancura Factor works.
The idea behind the Vancura factor is that in some parts of a heat, an
impedance regulator actually works better than a standard linear amps regulator.
However, rather than have 2 discrete modes of operation which would
require two sets of calibrations, William Vancura made the realization that changing the
method with which an Amp control signal was generated would allow a regulator to be
smoothly adjustable between an Amps Regulator and an Impedance Regulator. The
proof is as follows.
The equation for a standard Linear Amps Regulator is as
follows:
(1)
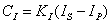
Where CI is the control signal for the Linear
Amps Regulator, KI is the gain, IS is the amps Setpoint
and IP is the actual Phase amps. .
(Note: All the equations have been constructed such that a positive
number in C corresponds to a request to lower the electrodes and increase
current flow.)
There are two types of impedance regulators.
One type regulates to true impedance and uses the following formula:
(2)
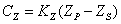or
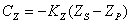
Where
(3)
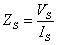and
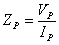
The other type of Impedance Regulator is actually only a
pseudo-impedance regulator or Difference Regulator. It actually regulates by summing a scaled magnitude of the
volts with a negative scaled magnitude of the amps.
It is adjusted so that, after scaling and the proper impedance is
reached, the control output is 0. Therefore,
from here on it will be referenced by calling it a Difference Regulator. This
uses the following equation:
(4)
.
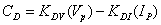Note: This is equivalent to an impedance regulator only
when CD= 0). The system always
strives to make CD= 0.
If you use a value to scale the volts to the same units as
amps (KIV), this can be rewritten as
(5)
.
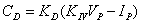The Vancura factor modifies IS by using the
equation:
(6)
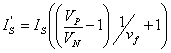
Where VN is the 3-phase average volts and vf
is the Vancura factor. There is
also some discussion as to whether the Vancura factor should be changed such
that 
which would change the equation to:
(7)
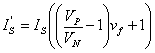
This allows vf to have the range 0-1 instead of
1->Infinity.
Using this method to calculate setpoint yields the
equation:
(8)
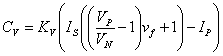
If you expand this out, you can get the equation.
(9)
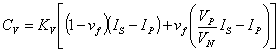
Which shows that, as vf goes to 0, the equation
becomes that of the Linear Amps Regulator:
(10)
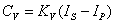
And, as vf goes to 1, it becomes the following
equation:
(11)
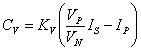
Which can be rewritten as
(12)
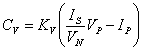
Which is identical to the Difference Regulator if
(13)
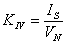
Then
(14)
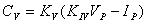Which is the same as
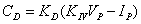
See (5) above.
One can make the assumption that VN = VS.
This is reasonably allowable, since it can be proven that, in worst-case
conditions, the error is only 15%. Then IS controls how much gain is
given to volts instead of amps, and KV is the gain of the regulator.
The error can be further reduced, if not eliminated, if the value VN
were computed from the phase-to-phase secondary volts. That is
(14a)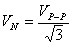
The Vancura factor is, therefore, continuously adjustable
between a pure Linear Amps Regulator and a pure Difference Regulator.
However, since the Difference Regulator is not a true
Impedance Regulator, it was decided to try and add a term to the equation to
accomplish this. The equation for the Vancura Regulator when the Vancura factor
is 1 can be written as:
(15)
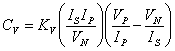
Again, making the substitution that VN = VS,
we can rewrite this as
(16)
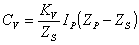
Since ZS is constant it can be incorporated into
the KV and clearly the only difference between this and an Impedance
regulator is the IP term. Therefore,
in order to turn the Difference Regulator into an Impedance Regulator all that
is needed is to divide by IP. However,
this changes the units and the gain of the formula. We can use a gain-normalized
version of IP, which is IP/IS, because IP
= IS whenever the system is at setpoint.
The original Vancura Regulator now becomes:
(17)
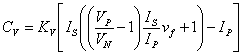
Since, however, we have determined that we would also like
the option to
continuously change between a Linear Amps regulator and an impedance-style
regulator, the idea was mentioned to be able to scale between a Difference
Regulator and an Impedance Regulator. Thus
the Meinel factor (mf) was introduced.
The Meinel factor is used to restrict the term IS/IP
in the above equation down to 1 when it is not desired.
The following equation was determined to cause the effect:
(18)
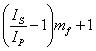
This yields the equation, which represents a triple mode
regulator based entirely on an amps setpoint for control simplicity:
(19)
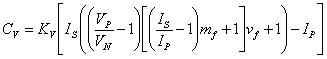
Where
(20)
(Amps) = 0 ≤ vf ≤
1 = ((Difference) = 0 ≤ mf
≤ 1 = (Impedance)).
As the Vancura factor (vf) is adjusted from 0 to
1 the formula transitions from a pure amps regulator to either a Difference
Regulator or an Impedance Regulator. If the Meinel factor (mf) is
zero, the equation will model a Difference Regulator and at one (1), it will
model an Impedance Regulator. Q.E.D.
Making Approximations: There
are two places in the above calculations where an assumption was made and the
action was justified only if specific conditions were met. The regulator
continuously strives to create the conditions required to make the assumptions
true, and the characteristics of the relationships produce only small
calculation errors when near the desired conditions. Additionally, the activity
of melting steel, using a plasma arc at 60 hertz, is so chaotic that all of the
input data (Volts and Amps) have to be heavily filtered in order to be of any
use whatsoever. Small calculation errors, in the order of 5% to 10%, become meaningless.
What is important, is that by making these assumptions, a highly practical
product was developed that substantially outperforms a difference regulator both
in operation, in ease of setup, and in maintainability.
My thanks to John Meinel who painstakingly worked through the math
to prove that the formula actually did what I said it would do.
William J. Vancura
